
Matemáticas a tu alcance
"Si la gente no piensa que las matemáticas son simples, es sólo porque no se dan cuenta de lo complicada que es la vida"
-John Louis von Neumann.
Matrices
Una empresa produce cuatro productos, A, B, C y D. El productor de cada artículo requiere cantidades específicas de dos materias primas, X y Y, y también cantidades determinadas de mano de obra. Suponga que la empresa desea comparar los números de unidades de X y Y y de mano de obra que se requieren en la producción semanal de estos cuatro productos. En la tabla 1 aparece información muestral para tal caso. Por ejemplo, la producción semanal de A requiere 250 unidades de X, 160 unidades de Y y 80 unidades de mano de obra.
Producto
a
b
c
d
Unidades material x
250
300
170
200
Unidades materiales y
160
230
75
120
Unidades mano obra
80
85
120
100
Este arreglo es ejemplo de una matriz. En este ejemplo, es claro que un arreglo rectangular es una forma natural en la cual almacenar los doce números dados. Cada columna de tres números en el arreglo se refiere a uno de los productos A, B, C o D; mientras que cada renglón de cuatro números se aplica a uno de los insumos X, Y o a la mano de obra. Así, el número 75 que está en el segundo renglón y la tercera columna da el número de unidades de la segunda materia prima (Y) usadas en la producción semanal del tercer producto (C). El número 80 en el tercer renglón y la primera columna representa el número de unidades del tercer insumo (mano de obra), que se requieren en la producción semanal del primer producto (A), etcétera. Una gran cantidad de otros conjuntos de datos tabulados forman naturalmente arreglos rectangulares. Veremos después que un buen número de cálculos que desearíamos realizar con tales datos corresponden a ciertas “operaciones con matrices” que se definen en esta sección y en las siguientes.
DEFINICIÓN
Una matriz es un arreglo rectangular de números reales, encerrado en grandes paréntesis rectangulares. Las matrices por lo regular se denotan con letras mayúsculas negritas como A, B o C.
Los números reales que forman el arreglo se denominan entradas o elementos de la matriz. Los elementos en cualquier línea horizontal forman un renglón y aquellos que se encuentran en cualquier línea vertical forman una columna de la matriz.
Una matriz que sólo tiene un renglón a menudo se conoce como matriz renglón o vector renglón. De manera similar, una matriz que sólo tiene una columna se denomina matriz columna o vector columna.
Matriz fila
Una matriz fila está constituida por una sola fila
Matriz columna
La matriz columna tiene una sola columna
Matriz rectangular
La matriz rectangular tiene distinto número de filas que de columnas, siendo su dimensión mxn
Matriz traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.
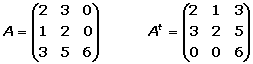
EJERCICIOS:
Para resolver estos ejercicios debemos aplicar las propiedades del producto de matrices, potencia de matrices, suma y resta de matrices, matriz identidad y matriz nula.


