
Matemáticas a tu alcance
"Si la gente no piensa que las matemáticas son simples, es sólo porque no se dan cuenta de lo complicada que es la vida"
-John Louis von Neumann.
Números Reales
NUMEROS REALES
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por R.
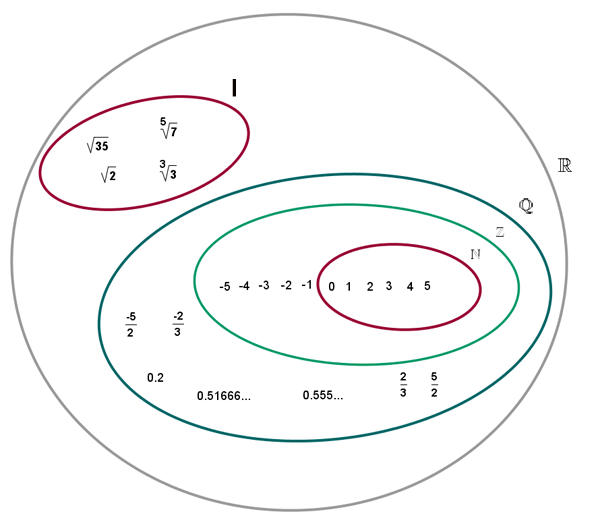
Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo, y la división por cero.
La recta real
A todo número real le corresponde un punto de la recta y a todo punto de la recta un número real.

Representación de los números reales
Los números reales pueden ser representados en la recta con tanta aproximación como queramos, pero hay casos en los que podemos representarlos de forma exacta.

Propiedades de la Suma de números reales
1 Interna:
El resultado de sumar dos números reales es otro número real.
a + b
+
2 Asociativa:
El modo de agrupar los sumandos no varía el resultado.
(a + b) + c = a + (b + c)
3 Conmutativa:
El orden de los sumandos no varía la suma.
a + b = b + a
4 Elemento neutro:
El 0 es el elemento neutro de la suma porque todo número sumado con él da el mismo número.
a + 0 = a
+ 0 =
Diferencia de números reales
La diferencia de dos números reales se define como la suma del minuendo más el opuesto del sustraendo.
a − b = a + (−b)
Producto de números reales
La regla de los signos del producto de los números enteros y racionales se sigue manteniendo con los números reales.
1 Interna:
El resultado de multiplicar dos números reales es otro número real.
2 Asociativa:
El modo de agrupar los factores no varía el resultado. Si a, b y c son números reales cualesquiera, se cumple que:
(a · b) · c = a · (b · c)
Conmutativa:
El orden de los factores no varía el producto.
a · b = b · a
Elemento neutro:
El 1 es el elemento neutro de la multiplicación, porque todo número multiplicado por él da el mismo número.
a ·1 = a
EJERCICIOS:


